Strukture podataka i algoritmi: Stabla

Strukture podataka i algoritmi

4.3 Stabla

4.3.1 Binarna stabla

Najjednostavniji oblik stabla je binarno stablo. Binarno stablo se sastoji od

cvora (zvanog korenski cvor) i
levog i desnog podstabla.
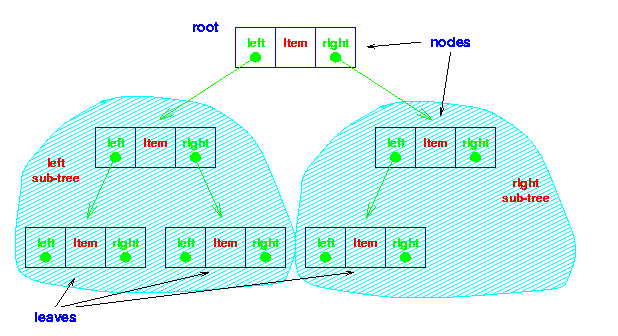
Oba podstabla su sama za sebe binarna stabla.

Sada imamo rekurzivno definisanu strukturu podataka. (Listu je takodje moguce definisati rekurzivno: znate li kako?)

Binarno stablo

Cvorovi na najnizim nivoima stabla (oni koji nemaju podstabla) zovu se listovi.

U uredjenom binarnom stablu,

kljucevi svih cvorova u levom podstablu su manji od onog u korenu,
kljucevi svih cvorova u desnom podstablu su veci od onog u korenu,
levo i desno podstablo su sama za sebe uredjena binarna stabla.

Struktura podataka

Struktura podataka za implementaciju stabala jednostavno dodaje "left" i "right" pointere umesto "next" pointera u implementaciji povezane liste. [Ucitaj strukturu stabla.]

Metod AddToCollection je naravno rekurzivan. [Ucitaj metod AddToCollection.]

Slicno, metod FindInCollection je takodje rekurzivan. [Ucitaj metod FindInCollection.]

Analiza

Kompletna stabla

Pre nego sto predjemo na opstije slucajeve, pretpostavimo (veoma optimisticno) da je nase stablo popunjeno na lep nacin, tj. da je svaki list na istom 'rastojanju' od korena.

Kompletno stablo

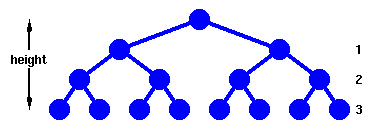Ovako se formira kompletno stablo, cija se visina definise kao broj veza (grana) od korena do najdubljeg cvora.

Najpre, treba da izracunamo koliko cvorova n, se nalazi u takvom stablu visine h.

Imamo da je

n = 1 + 2¹ + 2² + .... + 2^h

odakle je

n = 2^h+1 - 1

h = floor( log₂n )

Ispitivanje metoda FindInTree pokazuje da je u najgorem slucaju potrebno h+1 ili ceiling( log₂n ) poredjena da bi se pronasao objekat. Ovo je isto kao kod binarnog pretrazivanja.

Medjutim, AddToTree takodje zahteva ceiling( log₂n ) poredjenja da bi se odredilo gde treba dodati objekat. Kako ostatak obrade prilikom dodavanja objekata predstavlja konstantan broj operacija, kazemo binarno stablo zahteva O(logn) operacija i za dodavanje i za pretrazivanje objekata - sto je znacajno unapredjenje u odnosu na binarno pretrazivanje kada se radi o dinamickim strukturama koje zahtevaju cesto dodavanje novih objekata.

Brisanje je takodje O(logn) operacija.

Opsta binarna stabla

U opstem slucaju, dodavanje objekata u uredjeno stablo nece rezultirati kompletnim stablom. Najgori slucaj se dobija ako dodamo vec uredjeni niz objekata u stablo.

Sta ce se desiti? Razmislite pre nego sto kliknete ovde!

Ovaj problem se lako prevazilazi koriscenjem strukture poznate kao gomila (heap). No, pre nego sto se pozabavimo gomilama, formalizovacemo nase ideje o kompleksnosti algoritama pazljivo definisuci sta znaci O(f(n)).

Kljucni pojmovi

Koren: Cvor na "vrhu" stabla - onaj od koga pocinju sve operacije sa stablom. Ovaj cvor ne mora da postoji (kod praznog stabla je on jednak NULL), a kada postoji u binarnom stablu ima 0, 1 ili 2 potomka.
List: Cvor na "dnu" stabla - najdalji od korena. Listovi nemaju potomaka.
Kompletno stablo: Stablo u kome je svaki list na istom rastojanju od korena. Preciznija i formalnija definicija kompletnog stabla je data kasnije.
Visina: Broj veza (grana) koje moraju da se prodju na putu od korena do najdaljeg lista u stablu.