Strukture podataka i algoritmi: Gomile

Strukture podataka i algoritmi

6.2 Gomile

Gomile se zasnivaju na pojmu kompletnog stabla, za koje smo ranije dali neformalnu definiciju.

Formalno:

Binarno stablo je kompletno popunjeno ako ima visinu h i 2^h+1-1 cvorova.

Binarno stablo visine h je kompletno ako i samo ako je

prazno ili je

levo podstablo kompletno visine h-1 i desno podstablo je kompletno popunjeno visine h-2 ili je

levo podstablo kompletno popunjeno visine h-1 i desno podstablo je kompletno visine h-1.

Kompletno stablo se popunjava sa leve strane:

svi listovi su
- na istom nivou ili
- na dva susedna nivoa i
svi cvorovi na najnizem nivou se nalaze sto je moguce vise levo.

Gomile

Binarno stablo ima svojstvo gomile ako i samo ako je

prazno ili je
kljuc korena veci od kljuceva u potomcima i oba podstabla imaju svojstvo gomile.

Gomila moze da se koriste kao prioritetni red: objekat sa najvecim prioritetom se nalazi u korenu i trivijalno se vadi iz strukture. Ali ako se obrise koren, tada nam ostaju dva podstabla i moramo da ih efikasno spojimo u jedno stablo koje ce ponovo imati svojstvo gomile.

Vrednost strukture gomile je u tome da mozemo i da izvadimo objekat najviseg prioriteta i ubacimo novi u O(logn) vremenu.

Kako ovo radimo?

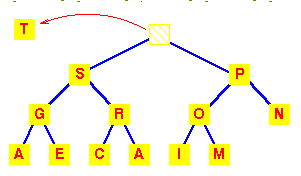
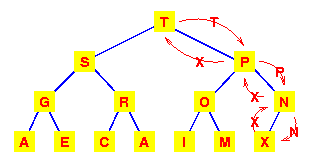
Pocnimo od sledece gomile.
Brisanjem se odstranjuje T
iz korena

Da bi videli kako cemo da odrzimo svojstvo gomile, koristimo cinjenicu da je kompletno stablo popunjeno sa leve strane. Prema tome, pozicija koja mora da postane prazna je ona na kojoj se nalazi M.
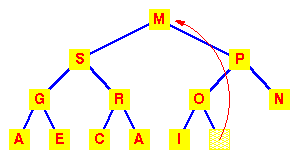
Zato M stavljamo na slobodno mesto u korenu.

Ovo je sada narusilo uslov da koren mora da bude veci od svojih potomaka.
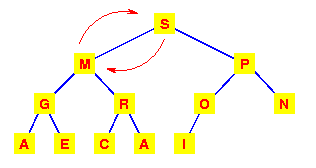
Zato M menjamo sa vecim od njegovih potomaka.

Sada je levo podstablo izgubilo svojstvo gomile.
Zato ponovo M menjamo sa vecim od njegovih potomaka.

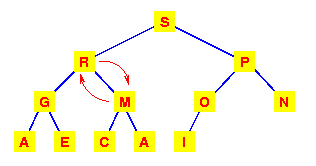Stablo sada ponovo ima svojstvo gomile, tako da smo zavrsili.

U ovom procesu je potrebno da izvrsimo najvise h izmena korena podstabla sa jednim od njegovih potomaka kako bismo u potpunosti vratili svojstvo gomile. Zato je za brisanje korena iz gomile potrebno O(h), odnosno O(logn) vreme.

Dodavanje na gomilu

Da bismo dodali objekat na gomilu, sledimo suprotnu proceduru.

Stavimo ga na mesto sledeceg lista sa desne strane i pomerajmo ga nagore dok ne uspostavimo svojstvo gomile.

Ponovo, za ovu proceduru je potrebno O(h), odnosno O(logn) zamena.

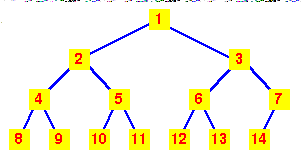Memorijsko predstavljanje kompletnih stabala

Svojstva kompletnog stabla vode do veoma efikasnog mehanizma za memorijsko predstavljanje koristeci n uzastopnih pozicija u nizu.

Ako numerisemo cvorove pocev od 1 u korenu i stavimo da je:

levi potomak cvora k na poziciji 2k
desni potomak cvora k na poziciji 2k+1

tada osobina 'popunjenosti s leve strane' kompletnog stabla osigurava da gomila moze da se smesti u uzastopnim pozicijama u nizu.

Posmatran kao niz, vidimo da se n-ti cvor uvek nalazi na n-tom mestu u nizu.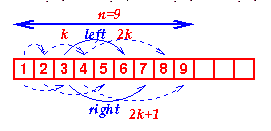

Kod za brisanje objekta sa najvisim prioritetom sa gomile je, naravno, rekurzivan. Jednom kada smo obrisali objekat iz korena (najvisi prioritet) i premestili poslednji objekat gomile u koren, jednostavno rekurzivno pozivamo metod MoveDown dok ne dodjemo do dna stabla.

Ucitaj heap_delete.c

Obratite paznju na makroe LEFT i RIGHT koji jednostavno predstavljaju relaciju izmedju indeksa cvora i njegovog levog i desnog potomka. Slicno, makro EMPTY predstavlja proveru da li je podstablo prazno ili ne.

Dodavanje na gomilu sledi slicnu strategiju, osim sto koristimo MoveUp funkciju da bismo upravo dodani objekat doveli do pravog mesta. (Za MoveUp funkciju bi se normalno dodao jos i makro koji definise PARENT za dati cvor.)

Gomile takodje daju i metod za sortiranje, poznat kao heapsort. Medjutim, najpre cemo prouciti i analizirati najjednostavniji metod za sortiranje.

Animacija

Primetite da su u animaciji prikazani i reprezentacija pomocu niza (koriscena u implementaciji algoritma) i (logicka) reprezentacija pomocu stabla. Ovo demonstrira kako se stablo rekonstruise da bi ponovo dobilo svojstvo gomile posle svakog dodavanja ili brisanja.

Animacija prioritetnog reda
Animaciju je napisao Woi Ang.

Posaljite komentare na adresu
morris@ee.uwa.edu.au

Kljucni pojmovi

Kompletno stablo
Balansirano stablo u kome je rastojanje od cvora do bilo kog lista ili h ili h-1.