1. prosecno vreme
2. vreme u najgorem slucaju i
3. najbolje moguce vreme.

Ako postoji n objekata u nasem skupu - bili oni smesteni kao niz ili kao povezana lista - tada je ocigledno da u najgorem slucaju, kada ne postoji objekat u skupu koji odgovara trazenom kljucu, moramo da napravimo n poredjenja datog kljuca sa kljucevima objekata u skupu.

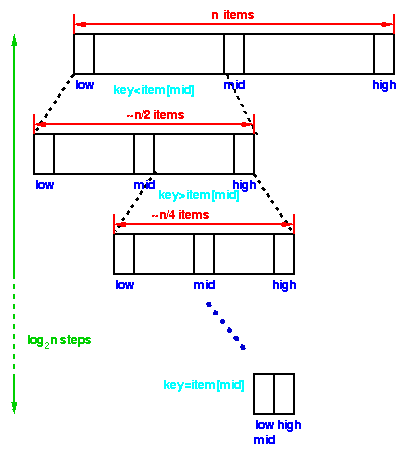
U binarnom pretrazivanju, najpre poredimo dati kljuc sa objektom na sredini niza. Ako je to trazeni objekat, mozemo da se vratimo istog trenutka. Ako je kljuc manji od kljuca objekta na sredini, tada trazeni objekat mora da se nalazi u donjoj polovini niza; ako je veci, tada trazeni objekat mora da se nalazi u gornjoj polovini niza. Stoga, proceduru ponavljamo na donjoj (ili gornjoj) polovini niza.

Nasa FindInCollection funkcija sada moze da se implementira ovako:

static void *bin_search( collection c, int low, int high, void *key ) {
	int mid;
	/* Uslov prekida */
	if (low > high) return NULL;
	mid = (high+low)/2;
	switch (memcmp(ItemKey(c->items[mid]),key,c->size)) {
		/* Slaganje, nasli smo objekat */
		case 0: return c->items[mid];
		/* kljuc je manji od mid, pretrazi donju polovinu */
		case -1: return bin_search( c, low, mid-1, key);
		/* kljuc je veci od mid, pretrazi gornju polovinu */
		case 1: return bin_search( c, mid+1, high, key );
		default : return NULL;
		}
	}

void *FindInCollection( collection c, void *key ) {
/* Trazi objekat u skupu
   Pre-uslov:
	(c je skup kreiran pozivom ConsCollection) &&
	(c je sortiran u rastuci poredak po kljucu) &&
	(key != NULL)
   Post-uslov: vraca objekat identifikovan kljucem ako postoji,
               u suprotnom vraca NULL
*/
	int low, high;
	low = 0; high = c->item_cnt-1;
	return bin_search( c, low, high, key );
}

1. bin_search je rekurzivna: ona odredjuje da li se trazeni objekat nalazi u donjoj ili gornjoj polovini niza, a zatim poziva samu sebe na odgovarajucoj polovini.
2. Postoji uslov prekida (u stvari, dva uslova!)
   1. Ako je low > high tada podniz koji treba pretraziti ne sadrzi nijedan element i
   2. Ako je dati kljuc jednak kljucu objekta u sredini trenutnog podniza, tada se takodje izlazi iz funkcije.
3. Funkcija AddToCollection mora da se modifikuje kako bi osigurala da se svaki dodati objekat nalazi na odgovarajucem mestu u nizu. Procedura je jednostavna:
   1. Pretrazi niz dok se ne nadje odgovarajuce mesto za ubacivanje novog objekta,
   2. Pomeri preostale objekte jedno mesto nadesno i
   3. Ubaci novi objekat na tako stvorenu praznu poziciju.
4. bin_search je deklarisana kao static. To je lokalna funkcija i ne koristi se van ove klase: ako ne bi bila deklarisana kao static, tada bi bila dostupna iz svih delova programa. Staticka deklaracija dozvoljava i drugim klasama da interno koriste isto ime za svoje funkcije!

   static smanjuje vidljivost funkcije i treba je koristiti kad god je moguce da bi se kontrolisao pristup funkcijama!

Analiza

Svaki korak algoritma deli pretrazivani podniz objekata na dva dela. Skup od n objekata mozemo da delimo na pola najvise log2 n puta. Stoga je vreme izvrsavanja binarnog pretrazivanja proporcionalno sa log n, pa kazemo da je ovo O(log n) algoritam.

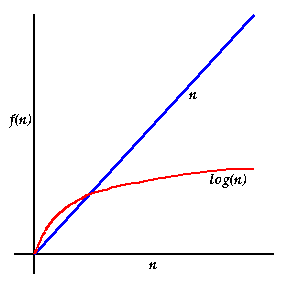
Binarno pretrazivanje zahteva slozeniji program nego nase originalno pretrazivanje, pa zato za male vrednost n ono moze da se izvrsava sporije nego jednostavno sekvencijalno pretrazivanje. Medjutim, za dovoljno veliko n, Stoga, za veliko n, log n je mnogo manji od n, pa je i O(log n) algoritam mnogo brzi od O(n) algoritma.

Grafici funkcija n i log n.