Strukture podataka i algoritmi: Crveno-crna stabla

Strukture podataka i algoritmi

8.2 Crveno-crna stabla

Crveno-crno stablo je binarno stablo pretrazivanja sa jos jednim dodatnom informacijom za svaki cvor: bojom, koja je ili crvena ili crna. Takodje je neophodno da vodimo racuna o roditelju svakog cvora, tako da bi struktura cvora crveno-crnog stabla bila:

struct t_red_black_node {
    enum { red, black } colour;
    void *item;
    struct t_red_black_node *left,
                     *right,
                     *parent;
    }

Tokom ovog razmatranja, NULL cvorove koji zavrsavaju stablo smatracemo listovima i obojene u crno.

Definicija crveno-crnog stabla

Crveno-crno stablo je binarno stablo pretrazivanja koje ima sledece crveno-crne osobine:

Svaki cvor je ili crven ili crn.
Svaki list (NULL) je crn.
Ako je cvor crven, tada su oba njegova potomka crna.
Svaki direktni put iz nekog cvora u bilo koji list ispod njega sadrzi isti broj crnih cvorova.

povlaci da duz svakog puta iz korena do lista, crveni cvorovi ne smeju da budu susedni.
Medjutim, bilo koji broj crnih cvorova moze da se pojavi jedan za drugim.

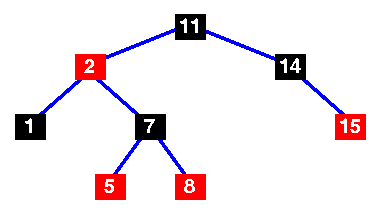
	Osnovno crveno-crno stablo
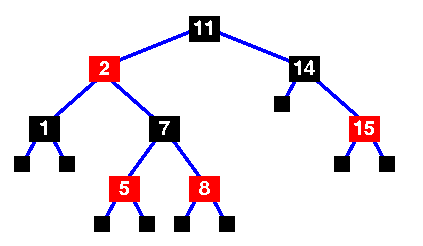
	Osnovno crveno-crno stablo sa dodatim strazarskim cvorovima. Implementacije algoritama sa crveno-crnim cvorovima obicno ukljucuju strazarske cvorove kao standardan nacin za prepoznavanje da se doslo do lista. Oni su, u stvari, crni NULL cvorovi iz osobine 2.

Broj crnih cvorova na svakom putu iz cvora x (ne ukljucujuci njega) do bilo kog lista, zove se crna visina cvora i oznacava sa bh(x). Moze se pokazati sledeca lema

Lema

Crveno-crno stablo sa n unutrasnjih cvorova ima visinu najvise 2log(n+1).

Sada se vidi zasto je crveno-crno stablo dobro stablo za pretrazivanje: ono se uvek moze pretraziti u O(log n) koraka.

Kao i sa gomilama, dodavanja i brisanja iz crveno-crnog stabla remete crveno-crne osobine, tako da ih je potrebno popravljati. Da bismo ovo uradili, neophodno je da pogledamo nekoliko operacija na crveno-crnim stablima.

Rotacija

Rotacija je lokalna operacija u stablu pretrazivanja koja ocuvava in-order poredak kljuceva.

Primetimo da u oba stabla, in-order obilazak daje:

A x B y C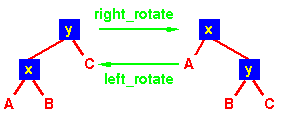

Operacija leve rotacije moze da se kodira na sledeci nacin:

left_rotate( Tree T, node x ) {
    node y;
    y = x->right;
    /* Pretvorimo levo podstablo cvora y u desno podstablo cvora x */
    x->right = y->left;
    if ( y->left != NULL )
        y->left->parent = x;
    /* Novi roditelj cvora y je bivsi roditelj cvora x */
    y->parent = x->parent;
    /* Roditelj treba da pokazuje na cvor y umesto na cvor x */
    /* Najpre proverimo da li se nalazimo u korenu - tada nema roditelja! */
    if ( x->parent == NULL ) T->root = y;
    else
        if ( x == (x->parent)->left )
            /* cvor x je bio sa leve strane svog roditelja */
            x->parent->left = y;
        else
            /* inace je cvor x morao da bude sa desne strane */
            x->parent->right = y;
    /* Konacno, stavimo cvor x sa leve strane cvora y */
    y->left = x;
    x->parent = y;
    }

Dodavanje

Dodavanje je relativno slozeno i ukljucuje veliki broj slucajeva. Primetimo da dodavanje novog cvora x u crveno-crno stablo pocinjemo na isti nacin kao sto bismo to uradili sa bilo kojim binarnim stablom, koristeci funkciju tree_insert. Ovaj novi cvor je obojen u crvenu boju, i mozda remeti crveno-crne osobine. U glavnoj petlji se tada penjemo uz stablo, dok ne oporavimo crveno-crne osobine.

rb_insert( Tree T, node x ) {
    /* Dodavanje u stablo na uobicajen nacin */
    tree_insert( T, x );
    /* Sada oporavi crveno-crne osobine */
    x->colour = red;
    while ( (x != T->root) && (x->parent->colour == red) ) {
       if ( x->parent == x->parent->parent->left ) {
           /* Ako je roditelj x sa leve strane, tada je y desni ujak cvora x */
           y = x->parent->parent->right;
           if ( y->colour == red ) {
               /* slucaj 1 - promeni boje */
               x->parent->colour = black;
               y->colour = black;
               x->parent->parent->colour = red;
               /* Pomeri x nagore kroz stablo */
               x = x->parent->parent;
               }
           else {
               /* y je crni cvor */
               if ( x == x->parent->right ) {
                   /* a x je sa desne strane */
                   /* slucaj 2 - pomeri x nagore i rotiraj */
                   x = x->parent;
                   left_rotate( T, x );
                   }
               /* slucaj 3 */
               x->parent->colour = black;
               x->parent->parent->colour = red;
               right_rotate( T, x->parent->parent );
               }
           }
       else {
           /* ponoviti "if" deo sa izmenjenim "right" i "left" */
       }
    /* Oboji koren u crno */
    T->root->colour = black;
    }

Ovde je primer operacije dodavanja.

Animacija

Animacija crveno-crnog stabla
Animaciju su napisali Linda Luo, Mervyn Ng, Anita Lee, John Morris i Woi Ang.

Posaljite komentare na adresu
morris@ee.uwa.edu.au

Studiranje koda otkriva samo jednu petlju. U toj petlji, cvor x u korenu podstabla cije crveno-crne osobine pokusavamo da oporavimo, moze biti pomeren nagore kroz stablo bar jedan nivo u svakoj iteraciji petlje. Posto je stablo u pocetku imalo visinu O(log n), postoji O(log n) iteracija. Procedura tree_insert takodje ima O(log n) slozenost, tako da procedura rb_insert sveukupno traje O(log n) koraka.

Kljucni pojmovi

Crveno-crna stabla: Stabla koja ostaju balansirana - i stoga garantuju O(logn) vreme pretrazivanja - u dinamickom okruzenju. Ili jos vaznije, posto se svako stablo moze re-balansirati - ali po visokoj ceni - stablo koje se moze re-balansirati u O(logn) koraka.