Strukture podataka i algoritmi: AVL stabla

Strukture podataka i algoritmi

8.3 AVL stabla

AVL stablo je jos jedan tip balansiranog stabla pretrazivanja. Dobilo je ime po svojim autorima, Adelson-Velskii-m i Landis-u, a to je ujedno bilo i prvo predlozeno dinamicki balansirano stablo. Kao i crveno-crna stabla, ni ona nisu savrseno balansirana, ali se parovi podstabala razlikuju po visini najvise za 1, odrzavajuci pritom O(logn) vreme pretrazivanja. Operacije dodavanja i brisanja takodje traju O(logn) koraka.

Definicija AVL stabla

AVL stablo je binarno stablo pretrazivanja koje ima sledece osobine: Podstabla svakog cvora razlikuju se po visini najvise za jedan. Svako podstablo je AVL stablo.
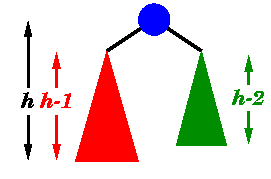
	Uslov balansiranja za AVL stablo: levo i desno podstablo razlikuju se po visini najvise za 1.

Morate biti pazljivi sa ovom definicijom: ona dozvoljava neka ocigledno nebalansirana stabla! Za primer, evo nekih stabala:

Stablo	AVL stablo?
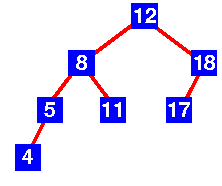	DA Ispitivanje pokazuje da svako levo podstablo ima visinu za 1 vecu od odgovarajuceg desnog podstabla.
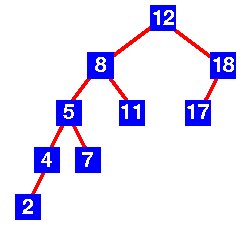	NE Podstablo sa korenom 8 ima visinu 4, dok podstablo sa korenom 18 ima visinu 2. Takodje, podstablo sa korenom 5 ima visinu 3, dok podstablo sa korenom 11 ima visinu 1.

Dodavanje

Kao i sa crveno-crnim stablima, dodavanje je relativno slozeno i uvodi dosta slucajeva. Implementacije dodavanja u AVL stablo se mogu naci u mnogim udzbenicima na engleskom: one se zasnivaju na dodatnoj informaciji, faktoru balansiranosti svakog cvora. Ovaj faktor oznacava da li je stablo levo-teze (visina levog podstabla je veca za 1 od desnog podstabla), balansirano (oba podstabla imaju istu visinu) ili je desno-teze (visina desnog podstabla je veca za 1 od levog podstabla). Ako se balansiranost poremeti dodavanjem cvora, tada se primenjuje rotacija za vracanje u stanje balansiranosti.

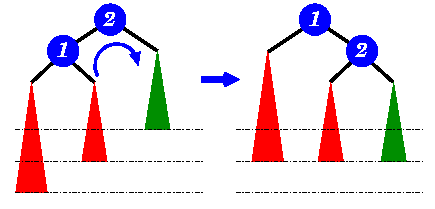Novi objekat je dodat u levo podstablo cvora 1, cineci da njegova visina postane veca za 2 od visine desnog podstabla cvora 2 (prikazanog u zelenoj boji). Primenom desne rotacije ispravlja se nebalansiranost.

Kljucni pojmovi

AVL stabla: Stabla koja ostaju balansirana - i stoga garantuju O(logn) vreme pretrazivanja - u dinamickom okruzenju. Ili jos vaznije, posto se svako stablo moze re-balansirati - ali po visokoj ceni - stablo koje se moze re-balansirati u O(logn) koraka.