Strukture podataka i algoritmi: Sortiranje

Strukture podataka i algoritmi

7 Sortiranje

Sortiranje je jedna od najvaznijih operacija koja se izvrsava na racunarima. U danima skladistenja podataka na magnetnim trakama pre modernih baza podataka, sortiranje je sigurno bilo i najcesca operacija koju su izvrsavali racunari, s obzirom da je azuriranje "baze podataka" ostvarivano sortiranjem transakcija i njihovim spajanjem sa glavnim fajlom. Ono je jos uvek vazno za predstavljanje podataka dobijenih iz baza: vecina ljudi voli da dobije izvestaje sortirane u nekom relevantnom poretku pre nego sto krene sa proucavanjem strana i strana podataka!

7.1 Sortiranje pomocu mehurova, umetanja ili izbora

Postoji veliki broj varijacija jedne osnovne strategije za sortiranje. To je ista strategija koju koristimo za sortiranje karti u preferansu. Dobijete kartu, pocnete od levog kraja ruke, pronadjete mesto gde treba ubaciti novu kartu, ubacite je i pomerite preostale karte za jedno mesto udesno.

/* Sortiranje celih brojeva umetanjem */

void insertion( int a[], int n ) {
/* Pre-uslov: a sadrzi n brojeva koje treba sortirati */
    int i, j, v;
    /* Na pocetku, prvi broj se smatra 'sortiranim' */
    /* i deli a u sortirani region x<i, i nesortirani deo x >= i */
    for(i=1;i<n;i++) {
        /* Izaberi broj na pocetku nesortiranog regiona */
        v = a[i];
        /* Idi unazad kroz niz, dok ne nadjes gde v treba da ide */
        j = i;
        /* Ako je ovaj broj veci od v,
              pomeri ga udesno */
        while ( a[j-1] > v ) {
          a[j] = a[j-1]; j = j-1;
          if ( j <= 0 ) break;
          }
        /* Zaustavljamo se kada je a[j-1] <= v, pa v stavljamo na mesto j */
        a[j] = v;
        }
    }

Animacija sortiranja umetanjem
Animaciju je napisao Woi Ang.

Posaljite komentare na adresu
morris@ee.uwa.edu.au

Sortiranje izborom

/* Sortiranje celih brojeva izborom */
#define SWAP(a,b)   { int t; t=a; a=b; b=t; }

void selection( int a[], int n ) {
/* Pre-uslov: a sadrzi n brojeva koje treba sortirati */
	int i, j, min;

	/* Na pocetku, ceo niz se smatra nesortiranim */
	for (i=0; i<n-1; i++) {
		/* nadji najmanji broj u nesortiranom delu niza */
		min = i;
		for (j=i+1; j<n; j++) {
			if (x[j]<x[min])
				min=j;
		}
		/* i postavi ga na pocetak nesortiranog dela niza */
		SWAP(x[min], x[i]);
	}
}

Sortiranje pomocu mehurova

Druga varijanta ove procedure, zvana sortiranje pomocu mehurova (bubble sort), se cesto izucava:

/* Sortiranje celih brojeva pomocu mehurova */
#define SWAP(a,b)   { int t; t=a; a=b; b=t; }

void bubble( int a[], int n )
/* Pre-uslov: a sadrzi n brojeva koje treba sortirati */
    {
    int i, j;
    /* Pravi n prolaza kroz niz */
    for(i=0;i<n;i++)
        {
        /* Od prvog elementa do kraja nesortiranog regiona */
        for(j=1;j<(n-i);j++)
           {
           /* Ako su susedni elementi u pogresnom poretku, zameni ih */
           if( a[j-1]>a[j] ) SWAP(a[j-1],a[j]);
           }
        }
    }

Analiza

Svaki od ovih algoritama zahteva n-1 prolaza: svaki prolaz stavlja jedan broj na ispravno mesto. (tada je n^-ti broj takodje na ispravnom mestu.) U i^-tom prolazu se pravi ili i ili n - i poredjenja i pomeranja. Prema tome:

ili O(n²) - ali mi vec znamo da mozemo da koristimo gomile da bi dobili O(n logn) algoritam. Stoga su ovi algoritmi pogodni samo za male probleme, gde ih njihov jednostavan kod cini brzim nego slozeniji kod O(n logn) algoritma. U sustini, ocekujte da ce O(n logn) algoritam biti brzi za n>10 - ali tacna vrednost veoma mnogo zavisi od konkretnog racunara!.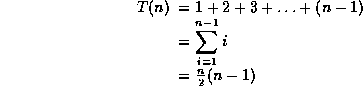

Ovi jednostavni algoritmi za sortiranje se takodje mogu koristiti kako bi iscedili i poslednju kap performansi iz brzih algoritama - videti kasnije.

Kljucni pojmovi

Sortiranje pomocu mehurova, umetanja ili izbora: Jednostavni algoritmi za sortiranje sa slozenoscu O(n²) - pogodni su jedino za sortiranje malog broja objekata.