Strukture podataka i algoritmi: Stekovi

Strukture podataka i algoritmi

3.3 Stekovi

Jos jedan nacin cuvanja podataka je u steku. Stek se obicno implementira sa samo dve glavne operacije (pored konstruktora i destruktora, naravno):

`push`	stavlja objekat na stek
`pop`	skida poslednji stavljeni objekat sa steka

Drugi metodi, kao sto su

`top`	vraca objekat na vrhu steka bez njegovog skidanja [9]
`isempty`	proverava da li je stek prazan

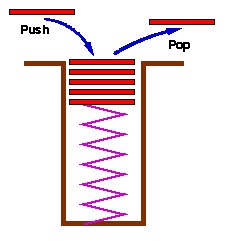
se takodje ponekad implementiraju.

Uobicajeni model steka je gomila tanjira. Tanjiri se "stavljaju" ("push") na vrh gomile, i "skidaju" ("pop") takodje sa vrha.
Stekovi obrazuju LIFO (Last-In-First-Out = Poslednji-Unutra-Prvi-Van) redove i imaju mnogo primena pocev od parsiranja algebarskih izraza do ...

Formalna specifikacija klase stek bi mogla da bude:

typedef struct t_stack *stack;

stack ConsStack( int max_items, int item_size );
/* Kreiraj novi stek
   Pre-uslov: (max_items > 0) && (item_size > 0)
   Post-uslov: vraca pointer na prazan stek
*/

void Push( stack s, void *item );
/* Stavlja objekat na vrh steka
   Pre-uslov: (s je stek kreiran pozivom ConsStack) &&
                  (postojeci broj objekata < max_items) &&
                  (item != NULL)
   Post-uslov: objekat je dodat na vrh steka s
*/

void *Pop( stack s );
/* Skida objekat sa vrha steka
   Pre-uslov: (s je stek kreiran pozivom ConsStack) &&
                  (postojeci broj objekata >= 1)
   Post-uslov: skinut je objekat sa vrha steka s
*/

Primetimo:

Stek je jednostavno jos jedan skup objekata, pa bi stoga bilo moguce koristiti istu specifikaciju kao i za opsti skup. Medjutim, skupovi sa LIFO semantikom steka su toliko vazni u racunarskoj nauci da ogranicena specifikacija steka nalazi svoju punu potvrdu.
Iako je moguce implementirati stek pomocu povezane liste (dodavanje i brisanje sa glave povezane liste daje upravo LIFO semantiku steka), najcesce primene steka imaju memorijsko ogranicenje, tako da je implementacija pomocu niza prirodnija i efikasnija (Kod vecine operativnih sistema, alokacija i de-alokacija memorije je relativno skupa operacija, tako da postoji nedostatak u brzini na racun fleksibilnosti implementacija pomocu povezane liste.).

3.3.1 Stek poziva

Po pravilu, programi kompajlirani u modernim jezicima visokog nivoa (cak i C!) koriste stek poziva za radnu memoriju svake pozvane procedure ili funkcije. Kada se pozove neka procedura ili funkcija, odredjeni broj reci - okvir poziva - se stavlja na stek poziva. Kada se vracamo iz procedure ili funkcije, ovaj okvir poziva se skida sa steka.

Kada funkcija poziva drugu funkciju, najpre se njeni argumenti, zatim adresa povratka i konacno prostor za lokalne promenljive stavljaju na stek poziva. Posto svaka funkcija radi u sopstvenom "okruzenju" ili kontekstu, postaje moguce da funkcija pozove samu sebe - tehnika poznata kao rekurzija. Ova mogucnost je ekstremno korisna - jer se mnogi problemi elegantno specificiraju ili resavaju na rekurzivan nacin.

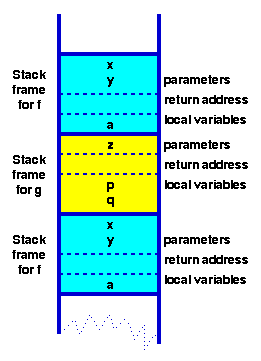Stek poziva posle izvrsavanja para uzajamno rekurzivnih funkcija:
function f(int x, int y) { int a; if ( term_cond ) return ...; a = .....; return g(a); } function g(int z) { int p,q; p = ...; q = ...; return f(p,q); }
Primetimo kako se celokupna okruzenja funkcija f i g (njihovi parametri i lokalne promenljive) nalaze na steku poziva. Kada se funkcija f pozove po drugi put iz funkcije g, kreira se novi okvir za drugi poziv funkcije f.

Kljucni pojmovi

push, pop: Opsti pojmovi za dodavanje, odnosno skidanje objekata sa steka
kontekst: Okruzenje u kome se izvrsava funkcija: sadrzi vrednosti argumenata, lokalne promenljive i globalne promenljive. Ceo kontekst, izuzev globalnih promenljivih, se smesta na stek poziva.
okvir poziva: Struktura podataka koja sadrzi sve podatke (argumente, lokalne promenljive, adresu za vracanje, itd.) potrebne svaki put kad se pozove procedura ili funkcija.