|
Strukture podataka i algoritmi
|
| 7.5 Radix Sort
|
Pristup Bin Sort-a moze da se uopsti u tehniku poznatu kao
radix sortiranje.
Primer
Pretpostavimo da imamo n celih brojeva u intervalu (0,n2),
koje treba sortirati.
(Kod Bin Sort-a, m = n2,
pa bismo imali O(n+m) = O(n2) algoritam.)
Sortirajmo ih u dve faze:
- Koristeci n kutija, stavimo ai u kutiju
ai mod n,
- Ponovimo proces koristeci n kutija,
ovaj put stavljajuci ai u kutiju
floor(ai/n),
pazeci da objekte dodajemo na kraj svake kutije.
Ovim se dobija sortirana lista.
Kao primer, posmatrajmo niz celih brojeva:
36 9 0 25 1 49 64 16 81 4
n je 10 i svi brojevi leze u opsegu (0,99).
Posle prve faze, imacemo:
| Kutija | 0 | 1 |
2 | 3 |
4 | 5 |
6 | 7 |
8 | 9 |
|---|
| Sadrzaj |
0 |
1
81 | - | - |
64
4 |
25 |
36
16 |
- |
- |
9
49 |
U ovoj fazi smo svaki objekat smestili u kutiju
indeksiranu najmanje znacajnom decimalnom cifrom - cifrom jedinica,
i dobili sledeci niz:
0 1 81 64 4 25 36 16 9 49
Ponavljajuci ovaj proces dobicemo:
| Kutija | 0 | 1 |
2 | 3 |
4 | 5 |
6 | 7 |
8 | 9 |
|---|
| Sadrzaj |
0
1
4
9 |
16 |
25 |
36 |
49 |
- |
64 |
- |
81 |
- |
U drugoj fazi smo koristili vodecu decimalnu cifru - cifru desetica,
da bismo brojeve smestili u kutije, vodeci pritom racuna da
svaki objekat dodajemo na kraj kutije.
Time smo dobili sortiran niz:
0 1 4 9 16 25 36 49 64 81
Ovaj proces mozemo da primenimo na brojeve proizvoljne velicine
koji su izrazeni u bilo kojoj osnovi (radix-u).
7.5.1 Uopsteni Radix Sort
Dalje mozemo da primetimo da cak nije neophodno koristiti istu osnovu
u svakoj fazi, pod pretpostavkom da kljuc, po kome se sortira,
predstavlja niz polja, svako sa ogranicenim opsegom.
Npr. ako je kljuc datum koji koristi strukturu:
typedef struct t_date {
int dan;
int mesec;
int godina;
} datum;
Ako se opsezi za dan i
mesec ogranice na ocigledan nacin,
a opseg za godinu se prigodno ogranici,
npr. 1900 < godina <= 2100,
tada mozemo da primenimo istu proceduru osim sto cemo
upotrebljavati razlicit broj kutija u svakoj fazi.
U svakom slucaju, najpre cemo sortirati po najmanje znacajnoj "cifri"
(gde "cifra" ovde oznacava polje sa ogranicenim opsegom),
zatim koristeci sledecu "cifru" po znacajnosti,
stavljajuci svaki objekat iza objekata koji se vec nalaze u kutiji,
i tako dalje.
Pretpostavimo da kljuc objekata koji se sortiraju ima k polja,
fi|i=0..k-1,
i da fi ima si diskretnih vrednosti,
tada se uopstena Radix Sort procedura moze zapisati na sledeci nacin:
radixsort( A, n ) {
for(i=0;i<k;i++) {
for(j=0;j<si;j++) bin[j] = EMPTY;
|
O(si) |
for(j=0;j<n;j++) {
pomeri Ai
na kraj kutije bin[Ai->fi]
} |
O(n) |
for(j=0;j<si;j++)
nadovezi bin[j] na kraj A;
}
} |
O(si) |
| Ukupno |
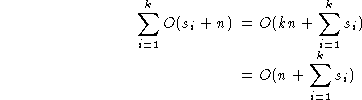 |
Sada ako su kljucevi, na primer, celi brojevi u opsegu (0,bk-1),
za neku konstantu k,
tada se kljucevi mogu posmatrati kao k-tocifreni brojevi po osnovi b.
Stoga je si = b za svako i i
vremenska kompleksnost postaje O(n+kb) ili O(n).
Ovaj rezultat zavisi od toga sto je k konstanta.
Ako bismo dozvolili da k raste sa n,
tada bi slika bila drugacija.
Na primer, potrebno je
log2n
binarnih cifara da se predstavi ceo broj <n.
Ako je dozvoljeno da duzine kljuceva rastu sa n,
tako da je k = logn,
tada bismo imali:
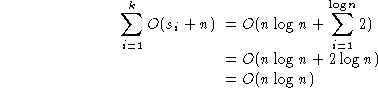 .
.
Jos jedan nacin da se gleda na ovo je da se primeti da
ako se opseg kljuceva ogranici na (0,bk-1),
tada se Radix Sort pristup moze koristiti efikasno
ako dozvolimo dupliranje kljuceva kada je
n>bk.
Medjutim, ako se neophodni jedinstveni kljucevi,
tada k mora da bude bar
logbn.
Stoga, ako se n uvecava, trebace nam logn faza,
od kojih svaka traje O(n) koraka,
tako da Radix Sort postaje isti kao i Quick Sort!
Animacija Radix Sort-a
Ovu animaciju je napisao Woi Ang. |
|
Posaljite komentare na adresu
morris@ee.uwa.edu.au
|
© John Morris, 1998.
Prevod sa engleskog,
Dragan Stevanovic, 2002.
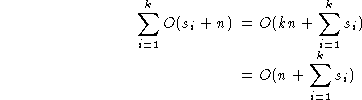
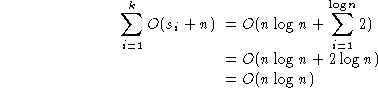 .
.