Strukture podataka i algoritmi: Hash tabele

Strukture podataka i algoritmi

8.5 Hash tabele

8.5.1 Tabele sa direktnim adresiranjem

Ako imamo skup od n elemenata ciji su kljucevi jedinstveni celi brojevi u intervalu (1,m), gde je m >= n, tada elemente mozemo da smestimo u tabelu sa direktnim adresiranjem T[m], gde je T_i ili prazno polje ili sadrzi jedan element iz naseg skupa.

Pretrazivanje tabele sa direktnim adresiranjem je ocigledno O(1) operacija: za kljuc k pristupamo polju T_k,

ako ono sadrzi element, vracamo ga
ako je prazno, vracamo NULL.

Ovde postoje dva ogranicenja:

kljucevi moraju da budu jedinstveni i
opseg kljuceva mora da bude ozbiljno ogranicen.

Ukoliko kljucevi nisu jedinstveni, tada mozemo jednostavno da kreiramo skup od m povezanih listi i da u polja tabele direktnog adresiranja smestimo adrese glava ovih listi. Vreme za nalazenje elementa koji odgovara ulaznom kljucu je i dalje O(1) - to je element sadrzan u glavi odgovarajuce liste.
Medjutim, ako elementi skupa imaju jos neku osobinu po kojoj se razlikuju (sem kljuca), i ako je maksimalan broj duplih kljuceva n_dup^max, tada trazenje odredjenog elementa traje O(n_dup^max) koraka. Ako su duplikati retki, tada je n_dup^max mnogo manje od n i tabela sa direktnim adresiranjem ce dati dobre performanse. Ali ako je n_dup^max istog reda velicine kao i n, tada trazenje odredjenog elementa traje O(n) koraka i koriscenje strukture stabla bi bilo mnogo efikasnije.

Opseg kljuceva odredjuje velicinu tabele direktnog adresiranja, koja moze da bude suvise velika da bi bila prakticna. Na primer, malo je verovatno da cete u sledecih par godina moci da koristite tabelu direktnog adresiranja za smestanje elemenata koji kao kljuceve imaju proizvoljne 32-bitne cele brojeve!

Direktno adresiranje se lako uopstava na slucaj kada postoji funkcija

h(k) => (1,m)

koja svaku vrednost kljuca k preslikava u interval (1,m). U ovom slucaju, element sa kljucem k smestamo u T[h(k)] (umesto u T[k]) i jos uvek mozemo da pretrazujemo u O(1) koraka kao i ranije.

8.5.2 Preslikavanje kljuceva

Pristup sa direktnim adresiranjem zahteva da je funkcija h(k) 1-1 preslikavanje iz skupa kljuceva u interval (1,m). Takva funkcija se naziva savrsena hash funkcija: ona preslikava svaki kljuc u razlicit ceo broj unutar nekog razumljivog opsega i omogucava nam da trivijalno napravimo tabelu sa O(1) vremenom pretrazivanja.

Na zalost, nalazenje savrsene hash funkcije nije uvek moguce. Recimo da mozemo da nadjemo hash funkciju h(k), koja preslikava vecinu kljuceva u jedinstvene brojeve, ali da manji broj kljuceva preslikava u isti broj. Ako je broj sudara (slucajeva kada se vise kljuceva preslikava u isti broj) dovoljno mali, tada hash tabele rade veoma dobro i daju O(1) vreme pretrazivanja.

Izbegavanje sudara

U malom broju slucajeva, kada se vise kljuceva preslikava u isti broj, elementi sa razlicitim kljucevima se mogu smestiti u isto polje hash tabele. Jasno je da je, u slucaju kada se hash funkcija koristi za lociranje elementa koji se trazi, neophodno poredjenje kljuca elementa sa datim kljucem. Medjutim, u istom polju tabele se sada moze naci vise od jednog elementa sa razlicitim kljucevima! Za resavanje ovog problema koriste se razlicite tehnike:

ulancavanje,
oblast prelivanja,
re-hashiranje,
koriscenje susednih polja (linearni preskok),
kvadratni preskok,
slucajni preskok, ...

Ulancavanje

Jedan jednostavan princip je da se svi sudari povezu u listu koja se prikaci na odgovarajuce polje. Ovako se moze rukovati neogranicenim brojem sudara i ne zahteva se unapred podatak o tome koliko elemenata se nalazi u skupu. Nedostatak je isti kao i kod implementacije skupa pomocu povezanih listi, umesto pomocu nizova: povezane liste traze vise prostora i, u manjem stepenu, vremena.

Re-hashiranje

Princip re-hashiranja koristi jos jednu hash funkciju kada dodje do sudara. Ako ponovo nastane sudar adresa, onda re-hashiramo dok se ne nadje prazno polje u tabeli.

Re-hash funkcija moze da bude ili sasvim nova funkcija ili ponovna primena originalne funkcije. Sve dok se funkcije primenjuju na kljuc u istom poretku, trazeni kljuc ce uvek moci da se nadje.

Linearni preskok

Jedna od najjednostavnijih re-hash funkcija je +1 (ili -1), tj. kad nastane sudar, pogledaj u susedno polje tabele. Nova adresa se racuna ekstremno brzo i moze biti ekstremno efikasna na modernim procesorima zahvaljujuci efikasnoj upotrebi kes memorije (videti diskusiju o efikasnosti povezanih lista).

Animacija prakticno prikazuje efekat linearnog preskoka: ona takodje implementira kvadratnu re-hash funkciju tako da se mogu proceniti razlike.

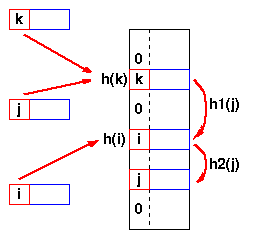
h(j)=h(k), pa se koristi sledeca hash funkcija h1. Nastaje i drugi sudar, pa se koristi sledeca hash funkcija h2.

Nagomilavanje

Linearni preskok je sklon fenomenu nagomilavanja. Re-hashirani elementi iz jednog polja zauzimaju blok polja u tabeli koji "raste" prema poljima koja zauzimaju drugi kljucevi. Ovo pogorsava problem sudara i broj re-hashiranih elemenata moze da postane veliki.

Kvadratni preskok

Bolje ponasanje se obicno dobija sa kvadratnim preskokom, gde sekundarna hash funkcija zavisi od re-hash indeksa: adresa = h(key) + c i² kod i^-tog re-hashiranja. (Slozenija funkcija od i se takodje moze koristiti.) Posto kljucevi, koji se preslikavaju u istu vrednost, slede isti niz adresa, kvadratni preskok pokazuje sekundarno nagomilavanje. Medjutim, sekundarno nagomilavanje je mnogo manje ozbiljno od nagomilavanja prouzrokovanog linearnim preskokom.

Re-hashing principi koriste originalno alociran prostor za tabele i stoga izbegavaju nedostatke povezanih listi, ali zahtevaju da se broj elemenata koje treba smestiti zna unapred.

Ipak, sudareni elementi se smestaju u polja u koja se drugi elementi preslikavaju direktno, tako da se potencijal za visestruke sudare povecava kako se tabela popunjava.

Oblast prelivanja

Ovaj princip deli pre-alociranu tabelu u dve oblasti: primarnu oblast u koju se preslikavaju kljucevi i oblast za sudare, koja se obicno zove oblast prelivanja.

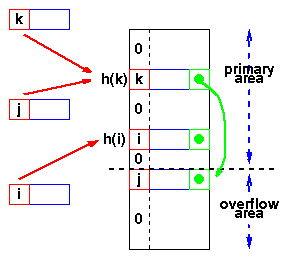Kada dodje do sudara, za novi element se koristi polje u oblasti prelivanja, a u primarnom polju se napravi pointer kao u povezanoj listi. Ovo je u sustini isto kao ulancavanje, osim sto je oblast prelivanja pre-alocirana i stoga moguce brza za pristup. Kao i sa re-hashiranjem, maksimalan broj elemenat mora biti poznat unapred, ali u ovom slucaju, moraju se proceniti dva parametra: optimalna velicina primarne oblasti i oblasti prelivanja.

Naravno, moguce je dizajnirati sisteme sa visestrukim oblastima prelivanja, ili sa mehanizmom za rukovanje sudarima u oblasti prelivanja, koja daju fleksibilnost bez gubitka prednosti oblasti prelivanja.

Rezime: organizacija hash tabele

Organizacija	Prednosti	Nedostaci
Ulancavanje	Neograniceni broj elemenata Neograniceni broj sudara	Gubitak zbog veceg broja povezanih listi
Re-hashiranje	Brzo re-hashiranje Brz pristup kroz koriscenje glavnog prostora tabele	Mora se znati maksimalni broj elemenata Visestruki sudari mogu postati verovatni
Oblast prelivanja	Brz pristup Sudari ne koriste primarni prostor tabele	Moraju se proceniti dva parametra koji uticu na performanse

Animacija

Animacija hash tabele
Animaciju je napisao Woi Ang.

Posaljite komentare na adresu
morris@ee.uwa.edu.au

Kljucni pojmovi

hash tabela: Tabela u kojoj objekat moze da se nadje u O(1) vremenu koristeci hash funkciju za dobijanje adrese pomocu kljuca.
hash funkcija: Funkcija koja, primenjena na kljuc, daje ceo broj koji se koristi kao adresa u hash tabeli.
sudar: Kada hash funkcija preslika dva razlicita kljuca u istu adresu u tabeli, kaze se da dolazi do sudara.
linearni preskok: Jednostavni princip za re-hashiranje u kome se prilikom sudara proverava da li je susedno polje slobodno da primi objekat.
kvadratni preskok: Princip re-hashiranja u kome se koristi funkcija hash indeksa viseg reda (obicno kvadratna) prilikom racunanja adrese.
nagomilavanje: Pojava nagomilavanja popunjenih susednih polja prilikom koriscenja linearnog preskoka.
sekundarno nagomilavanje: Nizovi sudara generisani adresama izracunatim pomocu kvadratnog preskoka.
savrsena hash funkcija: Funkcija koja, primenjena na sve objekte skupa koji treba smestiti u hash tabelu, daje skup jedinstvenih celih brojeva u nekom prihvatljivom intervalu.