Diskretna matematika

pismeni deo ispita

septembarsko - oktobarski  ispitni rok

16.9.2005. god.

1. Neka je B skup od b podskupova skupa 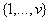, takav da svaki element skupa B ima tačno k elemenata i za svako 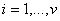 se element i nalazi u tačno r elemenata u B. Dokazati .
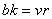2. Funkcija 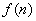 je definisana za svako 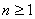 relacijom

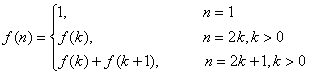
Neka je  generatorna funkcija niza . Dokazati da je , a odatle da je .

3. Ako k – regularan bipartitan graf G ima biparticiju (X, Y), dokazati da je .
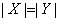4. Dokazati ili opovrgnuti tvrđenje: Ako je G Ojlerov graf koji sadrži grane e i f koje imaju zajednički čvor, onda G sadrži Ojlerovu konturu u kojoj se e i f pojavljuju neposredno jedna iza druge.
5. Dokazati da stablo ima najviše jedno savršeno sparivanje.

Rezultati:                    utorak, 20.9.2005. god. u 12.00