Diskretna matematika
pismeni deo ispita
septembarski ispitni rok
26.8.2005. god.
REŠENJA
- Neka je na
turniru učestvovalo m majstora i v velemajstora. Broj poena
osvojenih u partijama koje su međusobno igrali majstori je
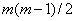 ,
a broj poena osvojenih u partijama koje su međusobno igrali velemajstori
je
,
a broj poena osvojenih u partijama koje su međusobno igrali velemajstori
je 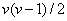 . Broj poena
osvojenih u partijama koje su igrali majstori protiv velemajstora je mv.
Kako je svaki igrač polovinu svojih poena osvojio igrajući protiv
majstora, to znači da je
. Broj poena
osvojenih u partijama koje su igrali majstori protiv velemajstora je mv.
Kako je svaki igrač polovinu svojih poena osvojio igrajući protiv
majstora, to znači da je 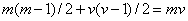 . Odatle sledi
. Odatle sledi 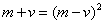 ,
tj. ukupan broj učesnika turnira je potpun kvadrat.
,
tj. ukupan broj učesnika turnira je potpun kvadrat. - Desna strana je broj načina za izbor k elemenata iz skupa od m + n elemenata. To se može uraditi i tako što se od prvih m elemenata izabere i, a od preostalih n izabere k – i elemenata, za svako i od 0 do k.
- Prvi graf
sadrži cikl
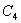 , dok ga druga
dva ne sadrže. Drugi i treći graf su izomorfni (...).
, dok ga druga
dva ne sadrže. Drugi i treći graf su izomorfni (...). - Postavimo
koordinatni sistem u jedan od uglova i svakoj kocki pridružimo trojku
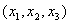 koordinata.
Zadatak je doći od kocke (0,0,0) do kocke (1,1,1) obilazeći tačno jednom
sve ostale kocke, gde je kretanje promena jedne od koordinata za 1.
Očigledno je minimalna dužina puta od (0,0,0) do
koordinata.
Zadatak je doći od kocke (0,0,0) do kocke (1,1,1) obilazeći tačno jednom
sve ostale kocke, gde je kretanje promena jedne od koordinata za 1.
Očigledno je minimalna dužina puta od (0,0,0) do 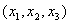 jednaka
jednaka
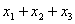 , a svi putevi
između ove dve kocke imaju istu parnost. Kada bi bilo moguće konstruisati
traženi put, on bi imao 27 čvorova, tj. 26 grana. Međutim, tada ne bi
mogao da se završi u (1,1,1) jer su svi putevi do (1,1,1) neparne dužine.
, a svi putevi
između ove dve kocke imaju istu parnost. Kada bi bilo moguće konstruisati
traženi put, on bi imao 27 čvorova, tj. 26 grana. Međutim, tada ne bi
mogao da se završi u (1,1,1) jer su svi putevi do (1,1,1) neparne dužine. - G je
Hamiltonov, pa sadrži cikl C koji prolazi kroz sve njegove čvorove.
Neka su čvorovi u X označeni sa
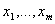 . Ciklu C
pridružimo jednu od dve moguće orijentacije. Neka je čvor
. Ciklu C
pridružimo jednu od dve moguće orijentacije. Neka je čvor 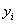 iza
čvora
iza
čvora 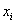 u ciklu C,
za svako
u ciklu C,
za svako 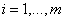 . Čvorovi
. Čvorovi 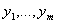 pripadaju
skupu Y jer u G nema grana sa oba kraja u X, a
pripadaju
skupu Y jer u G nema grana sa oba kraja u X, a 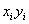 su
grane u G. Takođe, svi čvorovi
su
grane u G. Takođe, svi čvorovi 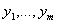 su mežusobno
različiti jer su na C, pa tvrđenje važi.
su mežusobno
različiti jer su na C, pa tvrđenje važi.