Diskretna matematika

pismeni deo ispita

septembarski ispitni rok

26.8.2005. god.

1. Na šahovskom turniru učestvovali su majstori i velemajstori. Svaka dva učesnika turnira su međusobno odigrali po jednu partiju. Ako je svaki učesnik turnira tačno polovinu svojih poena osvojio u partijama koje je igrao protiv majstora, dokazati da je broj učesnika turnira potpun kvadrat (pobednik u partiji dobija 1 poen, a u slučaju remija, oba igrača dobijaju po pola poena).
2. Dokazati da važi: .
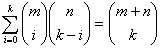3. Koji od sledećih grafova su međusobno izomorfni?

4. Data je kocka dimenzija 3x3, podeljena na manje kocke dimenzija 1x1. Da li postoji način da se polazeći od jedne od kocki u nekom uglu obiđu sve manje kocke tačno jednom i zavri put u kocki u sredini? Iz svake kocke je moguće preći na kocke koje sa njom imaju zajedničku stranu.
5. Neka su čvorovi grafa G podeljeni na dva disjunktna skupa X i Y, tako da ni jedna grana grafa G nema oba kraja u X. Ako je G Hamiltonov graf, dokazati da je .

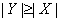Rezultati:                    ponedeljak, 29.8.2005. god. u 12.00