Diskretna matematika - pismeni deo ispita
junski ispitni rok (jun i)
07.06.2005.
1. Na koliko načina se n kuglica koje se međusobno ne razlikuju mogu razmestiti u m različitih kutija (m ≤ n), tako da važi:
a. Nijedna kutija nije prazna.
- U prvoj kutiji je tačno k (k ≤ n) kuglica.
- Dokazati da je
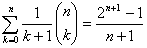 .
. - Neka je G graf sa n čvorova i m
grana takav da svi čvorovi imaju stepen k ili k + 1.
Ako G ima
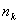 čvorova stepena k
i
čvorova stepena k
i 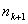 čvorova stepena k
+ 1, dokazati da je
čvorova stepena k
+ 1, dokazati da je 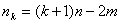 .
. - Dokazati da graf kome je svaki čvor parnog stepena ne sadrži most. Za svako k ≥ 1 konstruisati 2k + 1 – regularan graf koji sadrži most.
- Dato je 9 domina sa sledećim brojevima na sebi: (1,2), (1,4), (1,5), (1,6), (2,3), (2,4), (3,4), (4,5), (5,6). Dokazati da nije moguće rasporediti sve ove domine u krug, tako da se dodiruju po istim brojevima. Odrediti koliko je najmanje domina, kao i koje domine, potrebno dodati, tako da opisano raspoređivanje po krugu bude moguće.
Rezultati: četvrtak, 09.06.2005. godine u 11.00
Usmeni deo ispita: ponedeljak, 13.06.2005. godine u 12.00