Diskretna matematika

pismeni deo ispita

junski ispitni rok (jun II)

21.6.2005. godine

1. Na polici se nalazi n knjiga. Na koliko načina se može izabrati k knjiga, tako da nikoje dve izabrane knjige nisu susedne?
2. Neka su dati skupovi 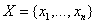 i .
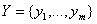1. Koliko ima surjektivnih funkcija ?
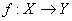2. Koristeći deo pod a. dokazati da važi
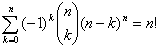
3. Ako su čvorovi u i v povezani u grafu G, rastojanje između njih 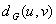 definišemo kao broj grana u najkraćem uv – putu. Ukoliko čvorovi u i v nisu povezani, rastojanje među njima je beskonačno. Dokazati da za svaka tri čvora u, v i w važi .
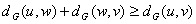4. Dokazati da je graf G stablo ako i samo ako je povezan i za svako 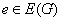 graf 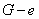 nije povezan.
5. Neka je n neparan broj. Dokazati da skakač ne može, krećući se po pravilima šaha, da obiđe celu šahovsku tablu dimanzija n × n, tako da na svako polje stane tačno jednom i da kretanje završi na početnom polju.

Rezultati:                    četvrtak, 23.6.2005. god. u 11.00

Usmeni:                      utorak, 28.6.2005. god. u 10.30