Diskretna matematika

pismeni deo ispita

08.10.2004.

1. Na koliko načina se mogu poređati u niz brojevi 1,2,...,kn (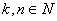), tako da svaki broj stoji na mestu čiji redni broj pri deljenju sa k daje isti ostatak kao i sam taj broj?
2. Korišćenjem metoda zmijskog ulja izračunati .
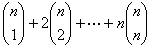3. Neka je G graf u kome je 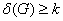, (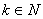). Dokazati da u G postoji put dužine bar k. Da li u G mora da postoji put dužine k+1?
4. Za grupu ljudi je poznato sledeće: ako dva čoveka imaju jednak broj poznanika, onda oni nemaju ni jednog zajedničkog poznanika. Dokazati da u toj grupi postoji čovek koji ima tačno jednog poznanika.
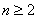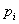5. Neka je T stablo sa n čvorova, . Za prirodan broj i, neka  označava broj čvorova stepena i u stablu T. Dokazati da je

.