Diskretna matematika

pismeni deo ispita

29.06.2004.

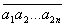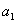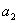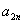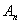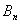1. Posmatramo skup svih brojeva oblika , gde su , ,..., cifre, s tim da brojevi mogu da počinju i nulama. Neka je  skup svih takvih brojeva kojima je zbir cifara jednak 9n, a  skup svih takvih brojeva kojima je zbir prvih n cifara jednak zbiru poslednjih n cifara. Dokazati da skupov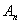i  i 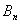 imaju isti broj elemenata.
2. U grupi ima n mladića i n devojaka. Oni su raspoređeni u vrstu na proizvoljan način. Na koliko načina mogu da se premeste (u okviru vrste), tako da ni jedan mladić ne ostane na mestu na kome je bio?
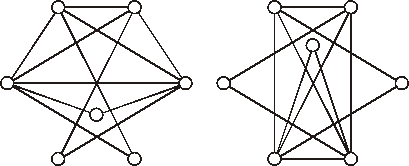
3.  Da li su grafovi na slici izomorfni? Obrazložiti odgovor.

4. Neka su 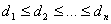 stepeni čvorova grafa G. Dokazati ga je G povezan graf ako je 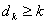 za svako .
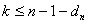5. Neka je T stablo u kome svaki čvor koji je susedan sa listom ima stepen bar 3. Dokazati da T ima par listova sa zajedničkim susedom.