DISKRETNA MATEMATIKA

II kolokvijum

27.05.2003.

1. Dokazati da svaki graf G koji ima bar jednu granu sadrži bar dva čvora koji nisu artikulacioni čvorovi.
2. Dokazati ili opovrgnuti : ako su i graf G i njegov komplement povezani, onda se G ili sastoji od samo jednog čvora, ili sardži 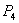 (put sa 4 čvora) kao indukovani podgraf.
3. Koji od sledećih grafova su međusobno izomorfni? Obrazložiti odgovor.

4. Graf koji ima jedinstveno razapinjuće stablo je stablo. Dokazati.